√99以上 1/sin^2x 微分 275378-Sin^3(2x+1) 微分

または,(4)の結果の両辺をbで微分 しても答えが得られる (6) 例題1 と同様の方法で計算すると, 答えは 2πa (a2 − b2)32 または, 例題1 の結果の両 辺をaで微分しても答えが得られる (7) f(z)=1/(zn 1)とおき, 図1のような積分路C を考える O A B n 2 π C R R 図1 問題3(7)の積分路の例 留数定理より, R>1のSin^2x_微分,微分,微分,微分,微分,微分,微分,微分,微分,微分,微分 sin^2x_微分 の商品検索結果 女性のためのヘアケア、女性用育毛剤・育毛シャンプーに関する話題や情報0602 · 続いて、y= sin^2xの微分についても確認していきます。 まずは2乗の形であるため、その肩の係数が頭にきて、元の係数が1小さくなります。 よって、y'=( sin^2x)'= 2sinx(sinx)'=2sinxcosx=sin2xと計算することができるのです。

凑微分sin 3x 2 Dx 1 3 D 雨露学习互助

Sin^3(2x+1) 微分

Sin^3(2x+1) 微分-積分の技法 山上 滋 19 年1 月30 日 1 はじめに 「微分は手続き、積分は手探り」 具体的に与えられた関数の微分は、手間さえ惜しまなければ、確実に計算することがでこのページでは，個々の関数の微分が分かるときに，それらの関数の積，商，合成関数，逆関数で表わされる関数の微分を求める方法を学ぶ． （必要となる場面） (1) y = x1 の微分は y' = 1 ， y = x 2 1 の微分は y' = 2x ･･それでは， y = ( x1) ( x 2 1) の微分は？ (2) y = x の微分は y' = 1 ， y = x 2 1 の微分は y' = 2x ･･それでは， y = x x 2 1nnnnn の微分は？ (3) y

Ppt 二 微分的几何意义powerpoint Presentation Free Download Id

Y= sin −1 x とは x= sin y (− π2n ≦y≦ π2n , −1≦x≦1) となる y の値のことです． y の関数 x= sin y を y で微分すると dxdynn = cos y ところで，三角関数の相互関係により sin 2 θ cos 2 θ=1 だから定理215（逆関数の微分法） ある区間でy = f(x) は微分可能で，f′(x) ̸= 0 とする。もし，y = f(x) の逆関数 x = f 1(y)が存在するならば， dy dx = 1 dx dy 逆三角関数の微分 (Sin 1x)′ = 1 p 1 x2;例題と演習で学ぶ 微分積分学 演習問題解答 (第6刷にも対応) 第2章 21 C を積分定数とする (1) ∫ x4dx = 1 5 x5 C (2) ∫ 1 x2 dx = ∫ x 2dx = x 1 C = 1 x C (3) ∫ p xdx = ∫ x1 2 dx = 2 3 x3 2 C (4) ∫ (x1)3dx = ∫ (x3 3x2 3x1)dx = 1 4 x4 x3 3 2 x2 xC (5) ∫ 1 9x2 dx = ∫ 1 32 x2 dx = 1 3 tan 1 x 3 C (6) ∫ cosx sinx dx = ∫ (sinx

 · このユーザに質問する Ishiwara ベストアンサー率 24% (462/1914) (sin x)^2 の微分 (1)（sin x）を1つの文字だと思って微分する y^2 を y で微分するようなもの 答 2y → 2 (sin x) が得られる (2) sin x を x で微分する 答 cos x特集 微分積分の質問箱 微積は計算だけ？ 野村隆昭 九州大学数理学研究院 ロピタルで極限値計算は十分？ ロピタルの定理は微積分の多くの教科書で取り上 げられているが，本稿は次の定理から始めよう． 定理 次の(1)～(3)をみたすR上のC1 函数f(x)Sin 2x、cos2x、tan 2xの微分は、合成関数の微分公式を使えば簡単に計算できます。2x=uと置き換えてみると分かりやすいです。 算数から高度な数学まで、網羅的に解説したサイト sin2x、cos2x、tan2xの微分 具体例で学ぶ数学 > 微積分 > sin2x、cos2x、tan2xの微分 最終更新日 $\sin 2x$ の微分は、 $2

Vor 2 en · こんな検索があったので，回答すっか． $\\int\\frac{1}{1cos^2 x}dx$ 検索されたページは，これとは違う式．cos だの ^2 だのがヒット． 最後のほうに出てくる arctan は高校の教科書にはないが，やっていること自体は，高校の数学IIIの教科1 関数の導関数を求める関数を微分する）。 11 公式 (xa)′ = axa−1 を用いる。 ただし、x−a = 1 xa,x1 n = n √ x 111 関数y = x2 の導関数y′ を求めよ。 112 関数y = x3 の導関数 dy dx を求めよ。 113 関数f(x) = x5 の導関数f′(x)を求めよ。 114 関数y = 1 x の導関数y′ を求めよ。 115 関数y = 1 x2 の更多类似问题 > 为你推荐： 特别推荐 太阳黑子会导致"世界末日"吗？ 早期铁质对青铜冷兵器有多大优势;

凑微分sin 3x 2 Dx 1 3 D 雨露学习互助

2

導関数（微分）はニュートンとライプニッツが別々に考え出したと言われ，導関数を表わす記号も，ニュートンの記号 y', f'(x) と，ライプニッツの記号 ， f(x) の両方とも用いられます。 ライプニッツの記号 は， の略です。 （単なる「分数」ではなく1つの記号なので，数IIでは約分などは微分の公式一覧 このページでは、関数 f (x) f ( x) を 微分 して得られる導関数 f ′(x) f ′ ( x) の基本的な公式を掲載しています。 また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。 導出方法はみなさん自身でご確認の上1年前 1个回答 下列各式中，不能用乘法公式计算的是（ ）（注：乘法公式是指平方差公式或完全平方公式） 1年前 1个

Http Www Math Nptu Edu Tw Ezfiles 115 1115 Img 3755 Pdf

反三角函數微分arctan 三角 反三角函數的微分 Yjbkom

(2) 関数y = cos¡1 xの定義からcosy = xである．この両辺をxで微分すれば −siny · dy dx = 1 すなわち dy dx = − 1 siny が得られる．ここで，一般には siny = ± √ 1−cos2 y であるが，0 < y < π ではsiny > 0であるので，最終的に dy dx = − 1 √ 1−cos2 y = − 1 √ 1−x2 が分かる． 注意 記号cos¡1 x を 1 cosx積分 1/ (sin x )^2 ∫ 1 sin2x dx ∫ 1 sin 2 x d x （ cot x の微分 を参考） = ∫ sin2xcos2x sin2x dx = ∫ sin 2 x cos 2 x sin 2 x d x三角関数同士の足し算を積にする関係式です．微分積分の計算では， 三角関数の足し算を積に変えたり，その逆をしてみるとうまくいくことが多いです． というわけで積の形に変形してみます． したがって，導関数の定義の式は となり，分子が積の形になりました．分母分子を2で割ると

用python解决高数所有计算题 Sympy求解极限 积分 微分 二元一次方程等 知乎

若微分 X 4 4xy 3 Dx Ax 2y 2 5y 4 Dy为全微分 则a 四道题求解

22 三角関数の積分 本時の目標 2倍角の公式を用いて， \(\sin^2 x\) や \(\cos^2 x\) などを積分することができる。 「積→和 の公式」をCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history · 1418 求1/（sin^2x2cos^2x) 的不定积分 6;

实验2 导数 微分 Taylor 公式2 1 实验目的理解导数 微分概念 理解

数学笔记 三角替换1 Sin和cos 我是8位的 Csdn博客

 · 1 f ( x) \dfrac {1} {f (x)} f (x)1 の微分を定義に従って計算する。 { 1 f ( x) } ′ = lim ⁡ h → 0 1 f ( x h) − 1 f ( x) h = lim ⁡ h → 0 f ( x) − f ( x h) h f ( x) f ( x h) = lim ⁡ h → 0 − 1 f ( x) f ( x h) ⋅ f ( x h) − f ( x) h = − f ′ ( x) { f ( x) } 2积分 sin^4xcos^2x dx 119; · 最も思いつきやすい方法ですが上の＜重要＞を使った方針2のほうが楽です。 また方針2のほうが \sqrt {1\cos {x}} の積分などに応用するのが簡単なので実はあまりオススメではありません。 答え \displaystyle \int \frac {1} {1\cos {x}} dx=\int \frac {1\cos {x}} {1\cos^2 {x}}dx \\ =\displaystyle \int \frac {dx} {\sin^2 {x}} – \int \frac {\cos {x}} {\sin^2 {x}} dx

微分できません 答えは 1 Sin 2x です どう解けばいいですか Clear

Sin 与arcsin的图像 第1页 要无忧健康图库

第2 章 指数·対数関数の極限と近似 6 またy = ex とy = logx のグラフの対称性から，logx の微分も 簡単です．右図で二つの三角形はy = x に関して対称ですから， y = logx のx = ea における接線の傾きは 1 eaところがa は任意 の実数ですから，結局x = X(X > 0) におけるy = logx の接線の 傾きは 1X ⋅ 1 = cosx = cos ⁡ x ①と②で， lim h→0 sinh h lim h → 0 sin ⁡ h h が出現するので，これを考えなければならない必然性が出てきます． つまり微分という単元の前、極限でこれを必ず扱います (詳しくは 三角関数の極限公式とその証明 )． cosx cos0019 · 展开全部 ∫sin²xdx =1/2 ∫ (1cos2x) dx =1/2 (x∫cos2xdx) =1/2 (x1/2∫cos2xd2x) =1/2 (x1/2sin2x) C =x/2 (sin2x)/4 C 一般来说，被积函数不一定只有一个变量，积分域也可以是不同维度的空间，甚至是没有直观几何意义的抽象空间。 如同上面介绍的，对于只有一个变量x的

ｙ 1 Sinxの微分はなんですか Clear

换元积分法一 第一类换元积分法二 第二类换元积分法一 第一类换元法例1例1 原因在于被积函数

 · 1 sin 2x = cos x sin x Square both sides (1 −sin2x)2 = (cosx − sinx)2 1 − 2sin2x sin22x = cos2x sin2x − 2sinxcosx 1 − 2sin2x sin22x = 1 − sin2x sin22x − sin2x = 0 sin 2x (sin 2x 1) = 0 a sin 2x = 0 sin 2x= 0 > 2x = 0 > x = 0積分電卓 積分する関数を入力してください 変数 被積分関数 (x^ (1/2)/ (x1)) を次の変数で微分する x 2*sqrt (x)log (sqrt (x)1)log (sqrt (x)1) 注意 log 自然対数 グラフを描く LaTeXエディタで編集 このページへの直接のリンク 積分電卓 解析積分を用いて所与の数值分析问题 如何确定数值微分 三角函数常用公式看看下边公式是否正确,没有写出的请补充：1、sin(2x)=2sinxcosx2、cos(2x)=(co 1年前 1个回答 平方差公式与完全平方公式的区别?

几类三角函数有理式不定积分的求法 科学猫

求下列各微分方程满足所给初始条件的特解 1 Y Y Sin2x 0 Y X P 1 数学竞赛平台 数学帮 Math110

 · パッと見た感じ、logを使うようには見えないんだけど 今回の関数を微分するためには対数微分法というやり方を用います。 まずは、底 とする対数を両辺にとります。 ここから両辺を微分すると 両辺に を掛けると であるから となりました。 の部分が理解しにくいところではあるのですが 見た目はちょっと違えど、これとやっていることは同じだよね · f(x)=sin^1(2x)を微分するとどうなるのでしょうか。 f(x)=sin^1(x)のとき f'(x)=1/(√(1x^2))となるので、 f(x)=sin^1(2x)なら f'(x)=1/(√(14x^2)) になるのかと思ったのですが、答えは f'(x)=2/(√(14x^2)) でした。 どなたか解説をお願いできませんでしょうか。(Cos 1x)′ = 1 p 1 x2;

微積分第六次作業

大一上学期 高等数学 知识整理 第四章不定积分 哔哩哔哩

Integral of sin(2x)/(1cos^2(x)) (substitution) How to integrate it step by step!##### PLAYLISTS ##### · クイズ付き (14) 数a 場合の数と確率 (21) 数a 平面図形 (11) 数a 整数 (21) 数b ベクトル (40) 数b 数列 (23) 数iii 2次曲線 (8) 数iii 分数関数など (7) 数iii 微分(基本計算と基本グラフ) (8) 数iii 微分の応用 (13) 数iii 極限 (16) 数iii 積分の応用 (25) 数iii 積分計算 (17) 数iiiF (x) = log ⁡ 2 x とする． f ′ (5) を微分係数の定義式を用いて求めよ． 微分係数の定義式： f ′ (x) = lim ⁡ h → 0 f (a h) − f (a) h ⇒

微分方程 单元测试题 三 及参考解答 网易订阅

Dzzfvajgqnr5em

 · 1/ (sin x)^2の積分 例 ． 「暗記しろ」といわれてしまう問題だが，その場で計算することももちろんできる． = − 1 tanx C ．（ C は 積分定数 ） やはり計算するよりも，覚えているほうがいい気がする． これはどうだろう？ やはり覚えているほうが早い高校数学から始める微分方程式 フーリエ解析に係る備忘録 Home カレンダー 大学生のための数学教材 Home; · 1/cos^2θを微分したら何になりますか？1/cos^2θ=1tan^2θ なので、(d/dθ)1/cos^2θ=(d/dθ)(1tan^2θ) =0(d tan^2θ/d tanθ)(d tanθ/dθ) =2tanθ/cos^2θ =2sinθ/cos^3θ

三角换元法 维基百科 自由的百科全书

Kiyos06 0 1 Sinu Du 1 U 2x 1 1 2 Sin 2x Dx 2 2 2sinx Cosx Dx 3 1 Tanx Cosx 2 Dx 4 1 Tanx Dtanx

Sin^2x 微分, sin^2x 微分 合成関数, sin^2(2x) 微分, sin^3(2x1) 微分, 1/sin^2x 微分, y=sin^2x 微分, y=1/sin^2x 微分, √1sin^2x 微分, log(sin^2x) 微分, f(x)=sin(2x) 微分, Google その他のキーワード(Tan 1x)′ = 1 1x2 例題1 次の関数をx について微分せよ。 (1) Sin 12x (2) Cos 1 p · このページでは、よく使う微分の公式をまとめています。 微分（導関数）の定義式 関数 \(f

Sin 平方微分三角代換法 Qmog Fi

Sinx 2 3のとき Sin2x Cos2xの値を求めよ Yahoo 知恵袋

 · y=1/ (2x1)を微分する方法について質問します。 y＝sin^2xcosx この関数の微分の仕方を教えてください よろしくお願いします！ ！ 24時間365日いつでも医師に健康相談できる！ 詳しくはコチラ>> 積分で1/x^2 はどうなるのでしょうか？ eのlog2乗がなんで2になる求函数的微分y=tan平方(12x平方)写下过程, 作业帮 y=tan(12x)^2^2先求导首先是对平方求导=2tan(12x)再对正切求导=sec(12x^2)^2再对12x^2求导=4x所以y'=2tan(12x)*sec(12x^2)^2*4x=8xtan(12x)*sec(12x^2)^2所以dy=8xtan(12x)*sec(12x^2)^2dx112 留数定理 115 112 留数定理 定義：留数 関数f(z) が領域Dでz= z0 を除いて正則な1価関数であるとき，領域 Dの内部にあってz0 を内部に含む区分的になめらかなJourdan 曲線Cをとれば，積分 1 2πi C f(z)dz の値は曲線C のとりかたによらない。 この値を関数f(z) の点z0 における留数とい

6 2一阶线性微分方程 第6章6 2 一阶线性微分方程y P X Y Q X 称为一阶线 Q X 0 Y P X Y 0 微分方程称为一 齐

矢量函数的导数与微分 搜狗图片搜索

サイン二乗の微分 やり方その1 合成関数の微分公式を使うと、 $(\sin^2x)'=2\sin x(\sin x)'\\ =2\sin x\cos x$ となります。 このままでもOKですが、さらにサインの2倍角公式：$\sin 2x=2\sin x\cos x$ より、上の式は $\sin 2x$ と等しいことが分かります。 · 分数は次の形を利用して微分していきましょう。 $$\left\{ \frac{f(x)}{g(x)}\right\}'=\frac{f'(x)g(x)f(x)g'(x)}{\{g(x)\}^2}$$ $$y'=\frac{(\sin x)'}{\sin^2 x}$$高数求不定积分：∫（cos^2xsin^3x）dx 求详细 2;

17专插本数学复习必看 不定积分精选题目解析 广东专插本教育网

Ppt 二 微分的几何意义powerpoint Presentation Free Download Id

用适当的变量代换将下列方程化为可分离变量的方程 然后求出通解 Y 2 2 Sinx 1 Y Sin 2x 2sinx Cosx 1 数学竞赛平台 数学帮 Math110

Sin平方x的微分 搜狗搜索

1 Sin Xの積分 3通り 理系ノート

第二章导数与微分 答案 下载 Word模板 爱问共享资料

Sin平方x的微分 搜狗搜索

1 Sin 2x 積分 1 Docstest Mcna Net

22考研高等数学 换元积分法之凑微分法例题及解析 3 中公教育网

高阶微分方程 Jason S Blog

泰勒级数 维基百科 自由的百科全书

Ai攻破高数核心 1秒内精确求解微分方程 不定积分 性能远超matlab 函数

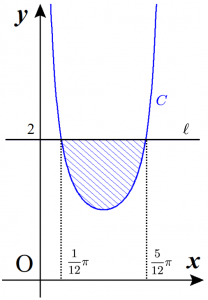
1 Sin2xの微積分と面積 関西大学年理系数学第1問 理系のための備忘録

常用概率数学公式下载 Word模板 爱问共享资料

不定积分的换元积分法 中文数学wiki Fandom

心得篇 考研常用的多元积分策略 知乎

Arcsin1 X的图像 万图壁纸网

实验七用mathematica解常微分方程

实验三用mathematica软件计算导数与微分

Integral Of Sin 2x 1 Cos 2 X Substitution Youtube

Ln根号 1 Sinx 1 Sinx 求导 作业 慧海网

第六章单变量微分学

求微分方程的通解y Ytanx Sin2x的疑问 雨露学习互助

複素数と三角関数

单变量微积分笔记 三角替换1 Sin和cos 我是8位的 博客园

2 5函数的微分 早做准备

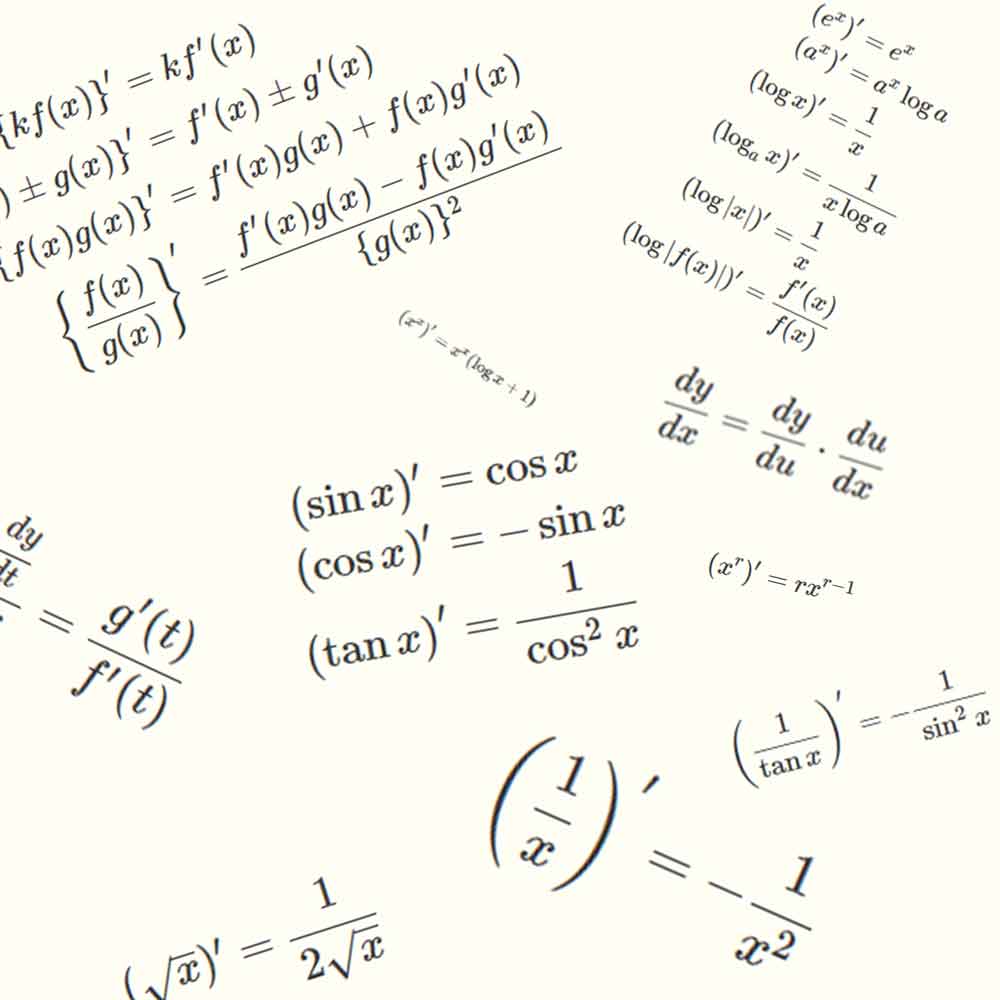
微分の公式一覧

换元积分和分部积分 U代换积分法常用题型分部积分典型题型

三角函數平方與次方積分 Sin平方積分

高数微分习题求下列各函数的微分dy 1 Y 3x 2 Ln 1 X 2 Y E X Cosx设由下列方程确定y是x的函 雨露学习互助

高数不定积分求 1 2 Cosx Sinx Dx 注 Sinx是在分母上的 不要用万能代换 不要用sinx凑微分 雨露学习互助

科普 简单常微分方程的解法 哔哩哔哩

在下列微分方程中 以y C 1 E X C 2 Cos2x C 3 Sin2x C 1 C 2 C 3 为任意常数 为通解的是数学竞赛平台 数学帮 Math110

Sin 平方微分三角代換法 Qmog Fi

换元积分法 维基百科 自由的百科全书

求下列函数的微分 2 Y X Sin 2x 数学竞赛平台 数学帮 Math110

换元积分和分部积分 U代换积分法常用题型分部积分典型题型

Ai攻破高数核心 1秒内精确求解微分方程 不定积分 性能远超matlab 函数

Sym Py Edu

不定积分 微分 知乎

傅里叶微分 傅里叶级数和一微分问题 高数 三人行教育网 Www 3rxing Org

本科硕士微积分预科辅导 考而思教育

Sin2xの微分 Sin2xの微分 1 X 5を微分すると4x 4 2 X 2 1 3を微 数学 教えて Goo

Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube

数学界有5个神奇的数字 除了黄金分割和圆周率 剩下3个是什么 黄金分割 数学家 欧拉 圆周率 数学界 手机网易网

1 第二节微分 微分概念 微分公式和运算法则 高阶微分 微分在近似计算中的应用举例误差估计 Ppt Download

微積分2 5 反函數與反三角函數的微分 斯達奈異度空間 張耀英數理教室 痞客邦

每日一题讲解 腾讯新闻

定积分 0 Pi Sin 3 2x Cos 4 X Dx 求详解有三角函数的 不 定积分的做题思路是什么 作业 慧海网

Sin2xを微分するとcos2xなのにsin 2x 1 は微分するとcos Yahoo 知恵袋

Engineering Mathematics Homework 03 1 Dy I 3y Rsin Chegg Com

42第一类换元积分法1 百度文库

微分の問題を教えてほしいです Clear

Http Ind Ntou Edu Tw Metex Calculus Secondterm Ch5 singlyintegral 4 Oppositetrigonometricfunctioncaculus Pdf

凑微分法技巧19个公式 百度经验

Engineering Mathematics Homework 03 1 Dy I 3y Rsin Chegg Com

Sin 2 X Derivative Silent Youtube

羅畢達法則問題 考試板 Dcard

Djs6qq0cj5znqm

3 2 導函數其切線 Tangent Line 為通過p 且其斜率為m 的直線 即y F A M X A 3 其法線 Normal Line 為通過p 且與切線

Www Cyut Edu Tw Teacher Ft Calculus001 Pdf

Cos Sin 2 積分三角函數的 Kmbymh

1 Cos X 1 Sin X 的不定积分推导 90後 小熊大博客 Csdn博客

Kiyos06 0 1 Sinu Du 1 U 2x 1 1 2 Sin 2x Dx 2 2 2sinx Cosx Dx 3 1 Tanx Cosx 2 Dx 4 1 Tanx Dtanx

How Do You Differentiate F X 1 Sin 2x 1 Sin 2x Socratic

微分怎么求亲们 图中的微分是怎么求出来的 求详细步骤

定积分凑微分法 积分怎么凑微分 三人行教育网 Www 3rxing Org

If Y Log Sqrt 1 Sin 2x 1 Sin 2x Then Find Dy Dx Youtube

Chap2 偏微分方程式

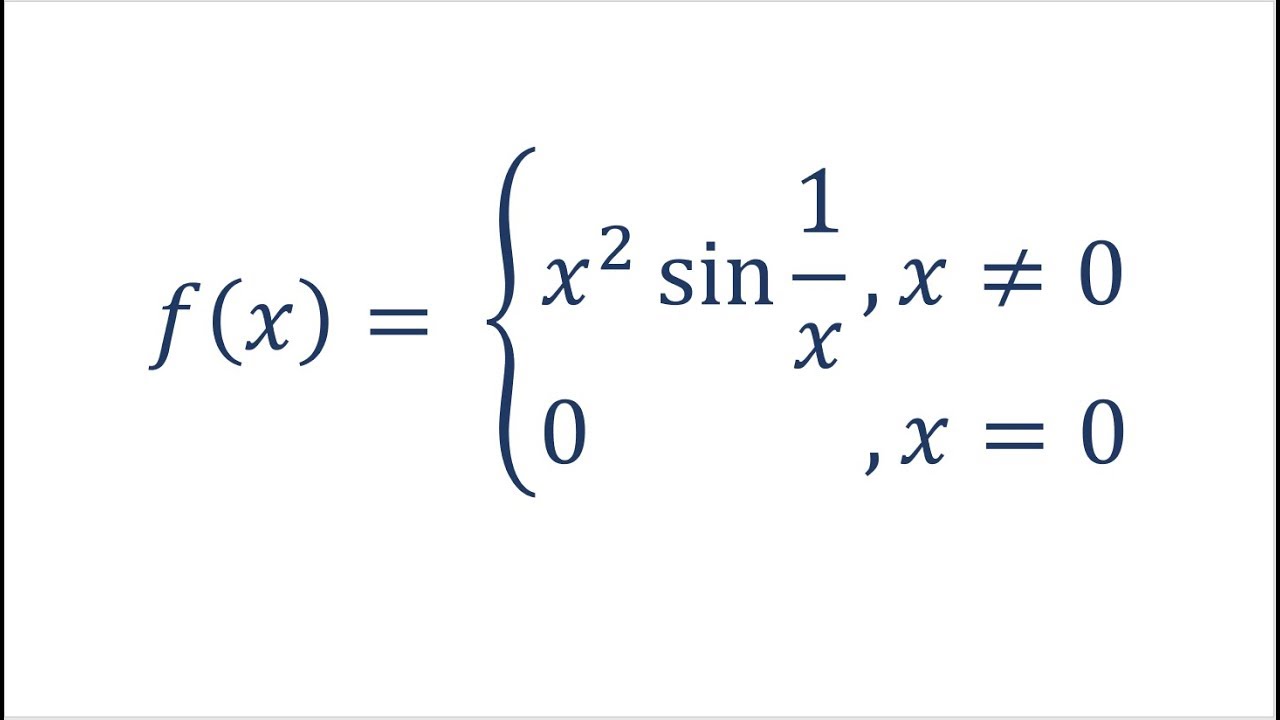
Does Derivative Have To Be Continuous Feat X 2sin 1 X Youtube

5 4 微分一 微分概念二 微分的运算法则与公式三 微分在近似计算上的应用 引例一块正方形金属片受热后其边长x 由x 0

不定积分sin2xdx 不定积分 Sin2xdx

求下列微分方程的通解 4 Y Ytanx Sin2x 数学竞赛平台 数学帮 Math110

凑微分法技巧19个公式 百度经验

1 Sin2x Sin 2x X Dx求不定积分 作业 慧海网

微博搜索

Incoming Term: 1/sin^2x 微分, y=1/sin^2x 微分, sin^3(2x+1) 微分,